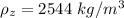Answer:
The density is
Step-by-step explanation:
From the question we are told that
The mass of the rock is
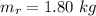
The tension on the string is
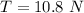
Generally the weight of the rock is
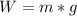
=>
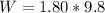
=>
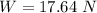
Now the upward force(buoyant force) acting on the rock is mathematically evaluated as
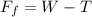
substituting values
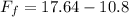

This buoyant force is mathematically represented as
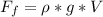
Here
 is the density of water and it value is
is the density of water and it value is
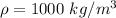
So
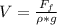

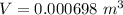
Now for this rock to flow the upward force (buoyant force) must be equal to the length

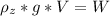
Here z is smallest density of a liquid in which the rock will float
=>
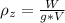
=>
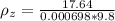
=>