Answer:
(A) The probability that a male spent less than $210 online before deciding to visit a store is 0.0668.
(B) The probability that a male spent between $270 and $300 online before deciding to visit a store is 0.0655.
(C) Ninety percent of the amounts spent online by a male before deciding to visit a store is less than $265.632.
Explanation:
We are given that the reports indicate that men spend an average of $240 online before they decide to visit a store. If the spending limit is normally distributed and the standard deviation is $20.
Let X = the spending limit
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = mean spending limit = $240
= mean spending limit = $240
 = standard deviation = $20
= standard deviation = $20
So, X ~ Normal(
 )
)
(A) The probability that a male spent less than $210 online before deciding to visit a store is given by = P(X < $210)
P(X < $210) = P(
 <
<
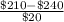 ) = P(Z < -1.50) = 1 - P(Z
) = P(Z < -1.50) = 1 - P(Z
 1.50)
1.50)
= 1 - 0.9332 = 0.0668
The above probability is calculated by looking at the value of x = 1.50 in the z table which has an area of 0.9332.
(B) The probability that a male spent between $270 and $300 online before deciding to visit a store is given by = P($270 < X < $300)
P($270 < X < $300) = P(X < $300) - P(X
 $270)
$270)
P(X < $300) = P(
 <
<
 ) = P(Z < 3) = 0.9987
) = P(Z < 3) = 0.9987
P(X
 $270) = P(
$270) = P(


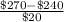 ) = P(Z
) = P(Z
 1.50) = 0.9332
1.50) = 0.9332
The above probability is calculated by looking at the value of x = 3 and x = 1.50 in the z table which has an area of 0.9987 and 0.9332 respectively.
Therefore, P($270 < X < $300) = 0.9987 - 0.9332 = 0.0655.
(C) Now, we have to find ninety percent of the amounts spent online by a male before deciding to visit a store is less than what value, that is;
P(X < x) = 0.90 {where x is the required value}
P(
 <
<
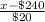 ) = 0.90
) = 0.90
P(Z <
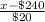 ) = 0.90
) = 0.90
In the z table, the critical value of z that represents the bottom 90% of the area is given as 1.2816, i.e;

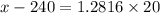
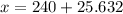
x = 265.632
Hence, Ninety percent of the amounts spent online by a male before deciding to visit a store is less than $265.632.