Explanation:
Hey, there!!!
Let me simply explain you about it.
We generally use the distance formula to get the points.
let the point R be (x,y)
As it an equilateral triangle it must have equal distance.
now,
let's find the distance of PQ,
we have, distance formulae is;

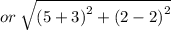
By simplifying it we get,

Now,
again finding the distance between PR,
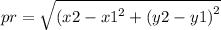
or,
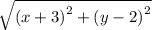
By simplifying it we get,
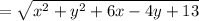
now, finding the distance of QR,
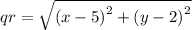
or, by simplification we get,
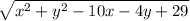
now, equating PR and QR,
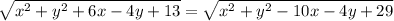
we cancelled the root ,
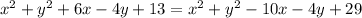
or, cancelling all like terms, we get,
6x+13= -10x+29
16x=16
x=16/16
Therefore, x= 1.
now,
equating, PR and PQ,
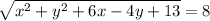
cancel the roots,

now,
(1)^2+ y^2+6×1-4y+13=8
or, 1+y^2+6-4y+13=8
y^2-4y+13+6+1=8
or, y(y-4)+20=8
or, y(y-4)= -12
either, or,
y= -12 y=8
Therefore, y= (8,-12)
by rounding off both values, we get,
x= 1
y=(8,-12)
So, i think it's (1,8) is your answer..
Hope it helps...