Question

The following situation will be used for the next three problems: A rock is projected upward from the surface of the moon, at time t = -0.0s, with a velocity of 30m/s. The acceleration due to gravity at the surface of the moon is 1.62m/s2 the time when the rock is ascending at a height of 180m is closest to:______.

a. 8s .
b. 12s.
c. 17s.
d. 23s.
e. 30s
For the previous situation, the height of the rock when it is descending with a velocity of 20m/s is closest to:_____.
A. 115m.
B. 125m.
C. 135m.
D. 145m
E. 155m.

Answer 1

Step-by-step explanation:

Given that,

Initial speed of the rock, u = 30 m/s

The acceleration due to gravity at the surface of the moon is 1.62 m/s².

We need to find the time when the rock is ascending at a height of 180 m.

The rock is projected from the surface of the moon. The equation of motion in this case is given by :

`h=ut-(1)/(2)gt^2\\\\180=30t-(1)/(2)* 1.62t^2`

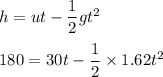
It is a quadratic equation, after solving whose solution is given by:

t = 7.53 s

or

t = 8 seconds

(e)If it is decending, v = -20 m/s

Now t' is the time of descending. So,

`v=-u+gt\\\\t=(v+u)/(g)\\\\t=(20+30)/(1.62)\\\\t=30.86\ s`

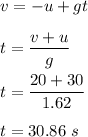
Let h' is the height of the rock at this time. So,

`h'=ut-(1)/(2)gt^2\\\\h'=30* 30.86-(1)/(2)* 1.62* 30.86^2\\\\h'=154.40\ m`

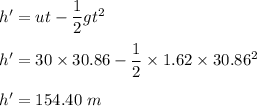
or

h' = 155 m