Answer:
Explanation:
Given that:
Let sample size of women be
 = 1000
= 1000
Let the proportion of the women be
 = 0.65
= 0.65
Let the sample size of the men be
 = 1000
= 1000
Let the proportion of the mem be
 = 0.60
= 0.60
The null and the alternative hypothesis can be computed as follows:
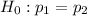

Thus from the alternative hypothesis we can realize that this is a two tailed test.
However, the pooled sample proportion p =
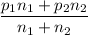
p =
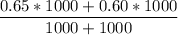
p =
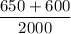
p = 0.625
The standard error of the test can be computed as follows:
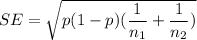
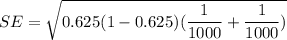
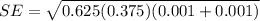
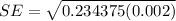

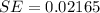
The test statistics is :
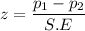
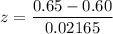

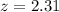
At level of significance of 0.05 the critical value for the z test will be in the region between - 1.96 and 1.96
Rejection region: To reject the null hypothesis if z < -1.96 or z > 1.96
Conclusion: Since the value of z is greater than 1.96, it lies in the region region. Therefore we reject the null hypothesis and we conclude that the percentage of men and women favoring a higher legal drinking age is different.