Question

What is the 8th term of the sequence? −16, 24, −36, 54, ... −729/8 2187/8 −2187/8 729/8

Answer 1

The answer is

`(2187)/(8)`

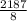
Explanation:

The sequence above is a geometric sequence

For an nth term in a geometric sequence

`A(n) = a ({r})^(n - 1)`

where n is the number of terms

r is the common ratio

a is the first term

From the question

a = - 16

To find the common ratio divide the previous term by the next term

That's

r = 24/-16 = -3/2 or -36/24 = - 3/2

Since we are finding the 8th term

n = 8

Substitute the values into the above formula

That's

`A(8) = - 16 ({ - (3)/(2) })^(8 - 1)`

`A(8) = - 16 ({ - (3)/(2) })^(7)`

`A(8) = - 16( - (2187)/(128) )`

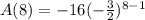
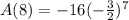
We have the final answer as

`A(8) = (2187)/(8)`

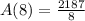
Hope this helps you