Question

Use the trick of Gauss to add up consecutive integers from 111 to 200200200, that is, find the sum 1+2+3+…+199+200 .\qquad\qquad\qquad 1+2+3+\ldots+199+200\;.1+2+3+…+199+200.

Answer 1

20100

Explanation:

To find the sum of:

`1 + 2 + 3+ 4+ ...... +200`

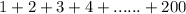
As per the trick of Gauss, let us divide the above terms in two halves.

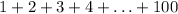`1+2+3+4+\ldots+100` and

`101+102+103+104+\ldots+200`

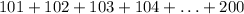
Let us re rewrite the above terms by reversing the second sequence of terms.

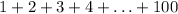`1+2+3+4+\ldots+100` (it has 100 terms) and

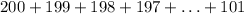`200+199+198+197+\ldots+101` (It also has 100 terms)

Adding the corresponding terms (it will also contain 100 terms):

1 + 200 = 201

2 + 199 = 201

3 + 198 = 201

:

:

100 + 101 = 201

The number of terms in each sequence are 100.

So, we have to add 201 for 100 times to get the required sum.

Required sum = 201 + 201 + 201 + 201 + . . . + 201 (100 times)

Required sum = 100
`*` 201 = 20100