Answer:
3.067MHz
Step-by-step explanation:
The formula for calculating the voltage across an inductor is expressed as
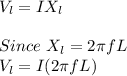
Given parameters
current amplitude I = 1.50mA = 1.5*10⁻³A
inductance L = 0.450mH = 0.450*10⁻³H
Voltage across the inductor
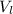 = 13.0V
= 13.0V
Required
frequency f
Substituting the given parametres into the formula, we have;
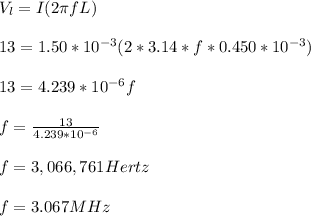
Hence, the frequency required is 3.067MHz