Question

What are the solutions of the equation x4 + 6x2 + 5 = 0? Use u substitution to solve.

x = i and x = i5
x=+ i and x
x= +115
O x=V-1 and x = = -5
x=+ -1 and x = = -5​

Answer 1

A; The first choice.

Explanation:

We have the equation
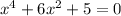`x^4+6x^2+5=0` and we want to solve using u-substitution.

When solving by u-substitution, we essentially want to turn our equation into quadratic form.

So, let
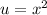`u=x^2`. We can rewrite our equation as:

`(x^2)^2+6(x^2)+5=0`

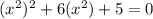
Substitute:

`u^2+6u+5=0`

Solve. We can factor:

`(u+5)(u+1)=0`

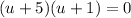
Zero Product Property:

`u+5=0\text{ and } u+1=0`

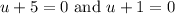
Solve for each case:

`u=-5\text{ and } u=-1`

Substitute back u:

`x^2=-5\text{ and } x^2=-1`

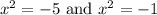
Take the square root of both sides for each case. Since we are taking an even root, we need plus-minus. Thus:

`x=\pm√(-5)\text{ and } x=\pm√(-1)`

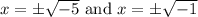
Simplify:

`x=\pm i√(5)\text{ and } x=\pm i`

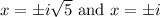
Our answer is A.