Answer:
Solution ( Second Attachment ) : - 2.017 + 0.656i
Solution ( First Attachment ) : 16.140 - 5.244i
Explanation:
Second Attachment : The quotient of the two expressions would be the following,
![6\left[\cos \left((2\pi )/(5)\right)+i\sin \left((2\pi \:)/(5)\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/800mvqma4nzapox91wf4quecmj9c3q8rs2.png) ÷
÷
![2√(2)\left[\cos \left((-\pi )/(2)\right)+i\sin \left((-\pi \:)/(2)\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/7pubdm0fstskot0qhh6hmdum2ktsu5uyj0.png)
So if we want to determine this expression in standard complex form, we can first convert it into trigonometric form, then apply trivial identities. Either that, or we can straight away apply the following identities and substitute,
( 1 ) cos(x) = sin(π / 2 - x)
( 2 ) sin(x) = cos(π / 2 - x)
If cos(x) = sin(π / 2 - x), then cos(2π / 5) = sin(π / 2 - 2π / 5) = sin(π / 10). Respectively sin(2π / 5) = cos(π / 2 - 2π / 5) = cos(π / 10). Let's simplify sin(π / 10) and cos(π / 10) with two more identities,
( 1 )
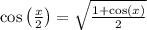
( 2 )
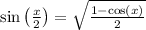
These two identities makes sin(π / 10) =
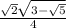 , and cos(π / 10) =
, and cos(π / 10) =
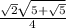 .
.
Therefore cos(2π / 5) =
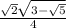 , and sin(2π / 5) =
, and sin(2π / 5) =
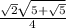 . Substitute,
. Substitute,
![6\left[ \left\frac{√(2)\sqrt{3-√(5)}}{4}+i\left\frac{√(2)\sqrt{5+√(5)}}{4}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/xc29w39e1ou9a3m3rlf1sylxzfm8fsyx7f.png) ÷
÷
![2√(2)\left[\cos \left((-\pi )/(2)\right)+i\sin \left((-\pi \:)/(2)\right)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/7pubdm0fstskot0qhh6hmdum2ktsu5uyj0.png)
Remember that cos(- π / 2) = 0, and sin(- π / 2) = - 1. Substituting those values,
![6\left[ \left\frac{√(2)\sqrt{3-√(5)}}{4}+i\left\frac{√(2)\sqrt{5+√(5)}}{4}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/xc29w39e1ou9a3m3rlf1sylxzfm8fsyx7f.png) ÷
÷
![2√(2)\left[0-i\right]](https://img.qammunity.org/2021/formulas/mathematics/college/x85a2i69x6vnc9d2dpcb73jo4us4t3mke4.png)
And now simplify this expression to receive our answer,
![6\left[ \left\frac{√(2)\sqrt{3-√(5)}}{4}+i\left\frac{√(2)\sqrt{5+√(5)}}{4}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/xc29w39e1ou9a3m3rlf1sylxzfm8fsyx7f.png) ÷
÷
![2√(2)\left[0-i\right]](https://img.qammunity.org/2021/formulas/mathematics/college/x85a2i69x6vnc9d2dpcb73jo4us4t3mke4.png) =
=
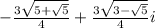 ,
,
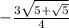 =
=
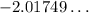 and
and
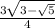 =
=
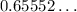
=
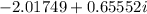
As you can see our solution is option c. - 2.01749 was rounded to - 2.017, and 0.65552 was rounded to 0.656.
________________________________________
First Attachment : We know from the previous problem that cos(2π / 5) =
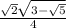 , sin(2π / 5) =
, sin(2π / 5) =
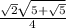 , cos(- π / 2) = 0, and sin(- π / 2) = - 1. Substituting we receive a simplified expression,
, cos(- π / 2) = 0, and sin(- π / 2) = - 1. Substituting we receive a simplified expression,
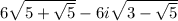
We know that
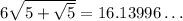 and
and
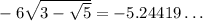 . Therefore,
. Therefore,
Solution :

Which rounds to about option b.