Question

Heidi bought a machine that throws tennis balls for her dog to fetch. The height of each ball thrown by the machine, in feet, is modeled by the function f(x) = –x2 + x + 2, where x represents time in seconds. How many seconds after the machine throws the ball does it hit the ground?

Answer 1

2 seconds

Explanation:

Given the equation:

`f(x) = -x^2 + x + 2`

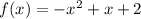
Where f(x) represents the height of each ball thrown by machine.

and x represents the time in seconds.

To find:

The number of seconds after which the machine throws the balls hits the ground = ?

Solution:

In other words, we have to find the value of
`x` after which the
`f(x) = 0`

(Because when the ball hits the ground, the height becomes 0).

Let us put
`f(x) = 0` and solve for
`x`

`f(x) = -x^2 + x + 2 =0\\\Rightarrow -x^2 + x + 2 =0\\\Rightarrow x^2 - x - 2 =0\\\Rightarrow x^2 - 2x+x - 2 =0\\\Rightarrow x(x - 2)+1(x - 2) =0\\\Rightarrow (x+1)(x - 2) =0\\\Rightarrow x =-1, 2`

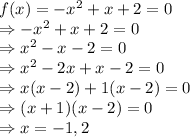
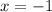`x=-1` sec is not a valid answer because time can not be negative.

So, the answer is after 2 seconds, the ball hits the ground.