Question

(SAT Prep) Find the value of x.

Answer 1

The value of x is 30°

Explanation:

We are given that the outer angle of the parallelogram is 60 degrees. Therefore it's respective inner angle will be 180 - 60 = 120 degrees. And, by properties of a parallelogram, the angle opposite to this angle will be 120 degrees as well.

If we draw extend the line creating angle 2x, then we will make ( 1 ) a vertical angle to 2x, ( 2 ) a 90 degree angle, and ( 3 ) and angle that we can let be y. Therefore, 2x + y = 90, and 3x + y = 120.

`\begin{bmatrix}2x+y=90\\ 3x+y=120\end{bmatrix}` ,

`\begin{bmatrix}6x+3y=270\\ 6x+2y=240\end{bmatrix}` ,

`6x+2y=240\\-\\\underline{6x+3y=270}\\y=30`,

`2x + (30) = 90,\\2x = 60,\\x = 30`

Solution : x = 30°

Answer 2

x = 30

Explanation:

a+ 60 = 180

a = 120

3x+b = 120 because opposite angles in a parallelogram are equal

2x+90+b = 180 since it forms a line

2x+b = 90

We have 2 equations and 2 unknowns

3x+b = 120

2x+b = 90

Subtracting

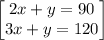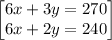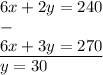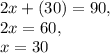
3x+b = 120

-2x-b = -90

---------------------

x = 30