Question

Solve for the unknown length.

Answer 1

Similar Triangles

Similar triangles have the same proportions of sides, but they have different side lengths.

To solve for missing sides in similar triangles, we can set up a proportion.

For instance, let's say that side a in Triangle A corresponds with side b in Triangle B. Let's say that side h in Triangle A also corresponds with side k in Triangle B. Then, it would be true that:

• 
  `(a)/(b)=(h)/(k)`

We need to make sure of a couple things:

• The numerators and denominators of fractions are corresponding
• The numerators describe one triangle, and the denominators describe another (can't switch, otherwise the calculations will get messed up)

Solving the Question

We're given two triangles (do you see it?).

• Triangle ABC
• Triangle ADE

These two triangles are similar.

We must solve for the length of side BC in Triangle ABC.

• We're given the length of DE, the corresponding side in Triangle ADE.
• We're also given the lengths of bottom sides, 20 units and 30 + 20 = 50 units.

Set up a proportion:

`(x)/(15)=(50)/(20)\\\\(x)/(15)=(5)/(2)\\\\x=(5)/(2)*15\\\\x=(75)/(2)\\\\x=37.5`

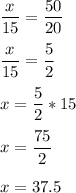
Therefore, the unknown length is 37.5 units.

Answer

37.5 units