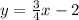Question

Please help! Find the equation of the line (graph provided in attached picture) Use exact numbers. y =_ x+_ ( _ represent blanks in the equation)

Answer 1

`y = (3)/(4)x - 2`

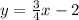
Explanation:

Equation of a line is given as
`y = mx + b`

Where,

m = slope of the line =
`(y_2 - y_1)/(x_2 - x_1)`

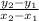
b = y-intercept, which is the value at the point where the line intercepts the y-axis. At this point, x = 0.

Let's find m and b to derive the equation for the line.

`m = (y_2 - y_1)/(x_2 - x_1)`

Use the coordinate pair of any two points on the line. Let's use the following,

`(0, -2) = (x_1, y_1)` => on the line, when x = 0, y = -2

`(4, 1) = (x_2, y_2)` => on the line, when x = 4, y = 1

Plug in the values and solve for m

`m = (1 - (-2))/(4 - 0)`

`m = (1 + 2)/(4)`

`m = (3)/(4)`

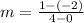
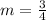
b = -2 (the line intercepts the y-axis at this point)

Our equation would be =>

`y = mx + b`

`y = (3)/(4)x + (-2)`

`y = (3)/(4)x - 2`