Answer:
The induced emf is

Step-by-step explanation:
From the question we are told that
The radius of the circular loop is
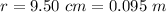
The intensity of the wave is
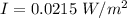
The wavelength is
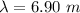
Generally the intensity is mathematically represented as
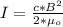
Here
 is the permeability of free space with value
is the permeability of free space with value

B is the magnetic field which can be mathematically represented from the equation as
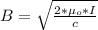
substituting values

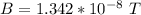
The area is mathematically represented as
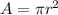
substituting values
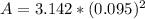
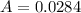
The angular velocity is mathematically represented as
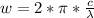
substituting values

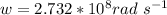
Generally the induced emf is mathematically represented as
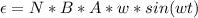
At maximum induced emf
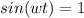
So
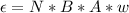
substituting values

