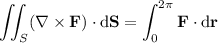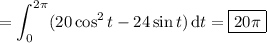Parameterize this surface (call it S) by
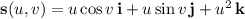
with
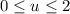 and
and
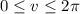 .
.
The normal vector to S is
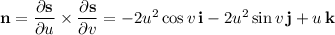
Compute the curl of F :
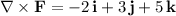
So the flux of curl(F) is
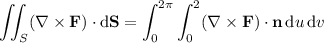
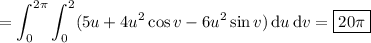
Alternatively, you can apply Stokes' theorem, which reduces the surface integral of the curl of F to the line integral of F along the intersection of the paraboloid with the plane z = 4. Parameterize this curve (call it C) by
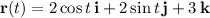
with
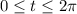 . Then
. Then