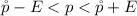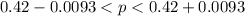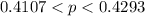Question

The amount of money spent on textbooks per year for students is approximately normal.

a. To estimate the population mean, 19 students are randomly selected the sample mean was $390 and the standard deviation was $120. Find a 95% confidence for the population meam.
b. If the confidence level in part a changed from 95% 1to1999%, would the margin of error for the confidence interval (mark one answer): decrease stay the same increase not enough information to answer
c. If the sample size in part a changed from 19 10 22. would the margin of errot for the confidence interval (mark one answer): decrease in stay the same increase in not enough information to answer
d. To estimate the proportion of students who purchase their textbookslused, 500 students were sampled. 210 of these students purchased used textbooks. Find a 99% confidence interval for the proportion of students who purchase used text books.

Answer 1

Answer:a

a

`336.04 < \mu < 443.96`

b

The margin of error will increase

c

The margin of error will decreases

d

The 99% confidence interval is
`0.4107 < p < 0.4293`

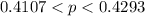
Explanation:

From the question we are told that

The sample size
`n = 19`

The sample mean is
`\= x = \$\ 390`

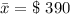
The standard deviation is
`\sigma = \$ \ 120`

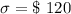
Given that the confidence level is 95% then the level of significance is mathematically represented as

`\alpha = 100 - 95`

`\alpha = 5 \%`

`\alpha = 0.05`

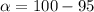
Next we obtain the critical value of
`(\alpha )/(2)` from the normal distribution table

So

`Z_{(\alpha )/(2) } = 1.96`

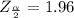
The margin of error is mathematically represented as

`E = Z_{(\alpha )/(2) } * (\sigma)/(√(n) )`

=>
`E = 1.96 * (120)/(√(19) )`

=>
`E = 53.96`

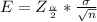
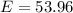
The 95% confidence interval is

`\= x - E < \mu < \= x + E`

=>
`390 - 53.96 < \mu < 390 - 53.96`

=>
`336.04 < \mu < 443.96`

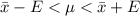
When the confidence level increases the
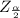`Z_{(\alpha )/(2) }` also increases which increases the margin of error hence the confidence level becomes wider

Generally the sample size mathematically varies with margin of error as follows

`n \ \ \alpha \ \ (1)/(E^2 )`

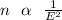
So if the sample size increases the margin of error decrease

The sample proportion is mathematically represented as

`\r p = (210)/(500)`

`\r p = 0.42`

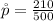
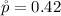
Given that the confidence level is 0.99 the level of significance is
`\alpha = 0.01`

The critical value of
`(\alpha )/(2)` from the normal distribution table is

`Z_{(\alpha )/(2) } = 2.58`

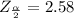
Generally the margin of error is mathematically represented as

`E = Z_{(\alpha )/(2) }* \sqrt{ (\r p (1- \r p ))/(n) }`

=>
`E = 0.42 * \sqrt{ (0.42 (1- 0.42 ))/( 500) }`

=>
`E = 0.0093`

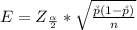
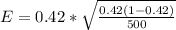
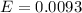
The 99% confidence interval is

`\r p - E < p < \r p + E`

`0.42 - 0.0093 < p < 0.42 + 0.0093`

`0.4107 < p < 0.4293`