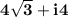Question

Use De Moivre's theorem to find the indicated power of the complex number. Write the answer in rectangular form.[2(cos10∘ + i sin10∘)]^3.

Answer 1

`\bold{4\sqrt3 + i4}`

Explanation:

Given complex number is:

`[2(cos10^\circ + i sin10^\circ)]^3`

To find:

Answer in rectangular form after using De Moivre's theorem = ?

i.e. the form
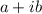`a+ib` (not in forms of angles)

Solution:

De Moivre's theorem provides us a way of solving the powers of complex numbers written in polar form.

As per De Moivre's theorem:

`(cos\theta+isin\theta)^n = cos(n\theta)+i(sin(n\theta))`

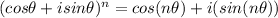
So, the given complex number can be written as:

`[2(cos10^\circ + i sin10^\circ)]^3\\\Rightarrow 2^3 * (cos10^\circ + i sin10^\circ)^3`

Now, using De Moivre's theorem:

`\Rightarrow 2^3 * (cos10^\circ + i sin10^\circ)^3\\\Rightarrow 8 * [cos(3 *10)^\circ + i sin(3 *10^\circ)]\\\Rightarrow 8 * (cos30^\circ + i sin30^\circ)\\\Rightarrow 8 * (\frac{\sqrt3}2 + i (1)/(2))\\\Rightarrow \frac{\sqrt3}2* 8 + i (1)/(2)* 8\\\Rightarrow \bold{4\sqrt3 + i4}`

So, the answer in rectangular form is:

`\bold{4\sqrt3 + i4}`