Answer:
The electron will get at about 0.388 cm (about 4 mm) from the negative plate before stopping.
Step-by-step explanation:
Recall that the Electric field is constant inside the parallel plates, and therefore the acceleration the electron feels is constant everywhere inside the parallel plates, so we can examine its motion using kinematics of a constantly accelerated particle. This constant acceleration is (based on Newton's 2nd Law:
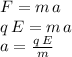
and since the electric field E in between parallel plates separated a distance d and under a potential difference
 , is given by:
, is given by:
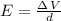
then :

We want to find when the particle reaches velocity zero via kinematics:

We replace this time (t) in the kinematic equation for the particle displacement:
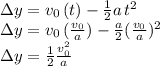
Replacing the values with the information given, converting the distance d into meters (0.01 m), using
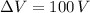 , and the electron's kinetic energy:
, and the electron's kinetic energy:
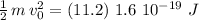
we get:
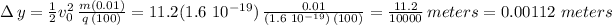 Therefore, since the electron was initially at 0.5 cm (0.005 m) from the negative plate, the closest it gets to this plate is:
Therefore, since the electron was initially at 0.5 cm (0.005 m) from the negative plate, the closest it gets to this plate is:
0.005 - 0.00112 m = 0.00388 m [or 0.388 cm]