Answer:

Explanation:
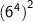
It is the example of Power to power law of indices.
Multiply the exponents
⇒
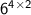
Multiply the numbers
⇒
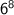
-------------------------------------------------------

If
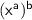 is an algebraic term then
is an algebraic term then
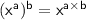
i.e When an algebraic term in the index form is raised to another index , the base is raised to the power of two indices.
Hope I helped!
Best regards!!