Answer:
The slope is -2, the y-intercept is 12
Explanation:
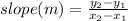
Chose any two coordinates pair. Let's make use of:
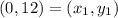

Thus,
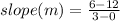
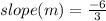
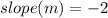
Using the slope-intercept equation, find the y-intercept, b, as follows:

Use any coordinate pair as x and y, then solve for b.
Let's use (3, 6)
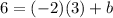
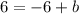
Add 6 to both sides
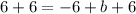
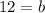
The slope (m) of the linear function that is represented by the table is -2, while the y-intercept (b), is 12.