Question

Find the values of θ in the range 0≤θ≤360° which satisfy: 2 sin^2 θ - sinθ -1= 0

Answer 1

Explanation:

Solving trig equations are just like solving "regular" equations. Let's get to it. First and foremost we are going to make a "u" substitution. You'll use that all the time in calculus, if you choose to go that route. Let

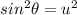`sin^2 \theta=u^2` and sinθ = u. Making the substitution, the equation becomes:

`2u^2-u-1=0`

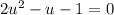
That looks like something that can be factored, right? If you throw it into the quadratic formula you get the factors:

(u - 1)(2u + 1) = 0

By the Zero Product Property, either u - 1 = 0 or 2u + 1 = 0, so we will solve those, but not until after we back-substitute!

Putting sinθ back in for u:

sinθ - 1 = 0 so

sinθ = 1 and in the other equation:

2sinθ + 1 = 0 so

2sinθ = -1 and

`sin\theta=-(1)/(2)`

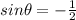
Get out the unit circle and look to where the sinθ has a value of 1. There's only one place in your interval, and it's at 90 degrees.

Now look to where the sinθ has a value of -1/2. There are 2 places within your interval, and those are at 210° and 330°. Now you're done!