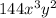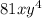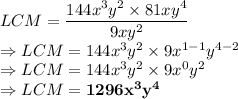Answer:
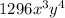
Explanation:
Given the terms:
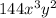
and
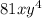
To find:
Greatest Common Divisor of the two terms or Least Common Multiple (LCM) of two numbers = ?
Solution:
First of all, let us find the HCF (Highest Common Factor) for both the terms.
i.e. the terms which are common to both.
Let us factorize them.
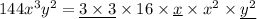

Common terms are underlined.
So, HCF of the terms =
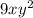
Now, we know the property that product of two numbers is equal to the product of the numbers themselves.
HCF
 LCM =
LCM =