Question

Determine the results of the following operations​

Answer 1

`\sqrt[3]{4}* (\sqrt[3]{16}-10 )`

Explanation:

Let be
`\sqrt[3]{64}-\sqrt[3]{32} * \sqrt[3]{125}`, this expression is simplified as follows:

1)
`\sqrt[3]{64}-\sqrt[3]{32} * \sqrt[3]{125}` Given

2)
`\sqrt[3]{4^(3)}-\sqrt[3]{2^(5)}* \sqrt[3]{5^(3)}` Definition of power

3)
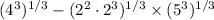`(4^(3))^(1/3)-(2^(2)\cdot 2^(3))^(1/3)* (5^(3))^(1/3)` Definition of n-th root/
`a^(b+c)= a^(b)\cdot a^(c)`/
`(a^(b))^(c) = a^(b\cdot c)`

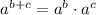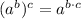
4)
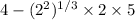
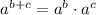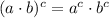
`4 - (2^(2))^(1/3)* 2* 5`
`a^(b+c)= a^(b)\cdot a^(c)`/
`(a\cdot b)^(c) = a^(c)\cdot b^(c)`

5)
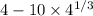`4 - 10* 4^(1/3)` Multiplication/Definition of power

6)
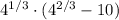`4^(1/3)\cdot (4^(2/3)-10)` Distributive property/
`a^(b+c)= a^(b)\cdot a^(c)`

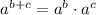
7)
`\sqrt[3]{4}* [(4^(2))^(1/3)-10]`
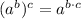`(a^(b))^(c) = a^(b\cdot c)`/Definition of n-th root

8)
`\sqrt[3]{4}* (\sqrt[3]{16}-10 )` Definition of power/Result