Question

A bag contains twelve marbles, which includes seven red marbles and five blue marbles. Roja reaches into the bag and pulls out four marbles. a) How many different sets of four marbles can be pulled from this bag? b) How many of these sets contain two red marbles and two blue marbles? c) How many of these sets contain all red marbles? d) How many of these sets contain all red marbles or all blue marbles?

Answer 1

a) 495

b) 210

c) 35

d) 40

Explanation:

Given a total of 12 marbles.

n = 12

Number of red marbles = 7

Number of blue marbles = 5

a) Number of different sets of 4 marbles that can be made from this bag ?

This is a simple combination problem.

where n = 12 and r = 4.

So, answer will be:

`_(12)C_4`

Formula:

`_(n)C_r = (n!)/((n-r)!r!)`

`_(12)C_4 = (12!)/((8)!4!) = (12* 11* 10* 9)/(4 * 3* 2) =\bold{495}`

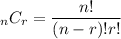
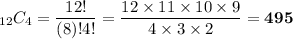
b) Two red and two blue marbles:

The answer will be:

`_(7)C_2 * _(5)C_2 = (7* 6)/(2) * (5* 4)/(2) =\bold{210}`

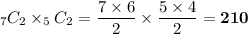
c) all red marbles.(4 chosen out of 7 red and 0 chosen out of 5 blue marbles)

`_(7)C_4 * _(5)C_0 = (7* 6* 5* 4)/(4* 3* 2) =\bold{35}`

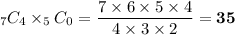
d) all red or all blue.(all red marbles plus all blue marbles)

All red marbles:

`_(7)C_4 * _(5)C_0 = (7* 6* 5* 4)/(4* 3* 2) * 1=\bold{35}`

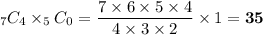
All blue marbles:

`_(7)C_0 * _(5)C_4 = 1 * (5* 4* 3* 2)/(4* 3* 2) =\bold{5}`

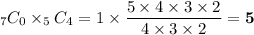
So, answer is 40.