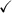Question

(k) 2 cos 16A + 1 = (2 cos 2A - 1).(2 cos 2A + 1).(2 cos 4A-1).(2cos 8A-1).

I need help to prove this......
Qno. k.​

Answer 1

Answer:Use the following Double Angle identity: cos 2A = 2cos²A - 1

We are going to find one factor at a time:

2 cos16A + 1 = (2cos2A - 1)(2cos2A + 1)(2cos4A - 1)(2cos8A - 1)

Explanation:

Answer 2

Answer: see proof below

Explanation:

Use the following Double Angle identity: cos 2A = 2cos²A - 1

We are going to find one factor at a time:

2 cos16A + 1 = (2cos2A - 1)(2cos2A + 1)(2cos4A - 1)(2cos8A - 1)

↓ ↓ ↓ ↓

factor last factor 2nd factor 1st

Proof LHS → RHS:

Given: 2 cos16A + 1

let α = 8A, then 2·cos2α + 1

Identity: 2(2cos²α - 1) + 1

Distribute: 4cos²α - 2 + 1

Simplify: 4cos²α - 1

Factor: (2cosα - 1)(2cosα + 1)

Substitute: (2cos8A - 1)(2cos8A + 1)

let β = 4A, then 2·cos2β + 1

Identity: 2(2cos²β - 1) + 1

Distribute: 4cos²β - 2 + 1

Simplify: 4cos²β - 1

Factor: (2cosβ - 1)(2cosβ + 1)

Substitute: (2cos4A - 1)(2cos4A + 1)

let Ф = 4A, then 2·cos2Ф + 1

Identity: 2(2cos²Ф - 1) + 1

Distribute: 4cos²Ф - 2 + 1

Simplify: 4cos²Ф - 1

Factor: (2cosФ - 1)(2cosФ + 1)

Substitute: (2cos2A - 1)(2cos2A + 1)

(2cos2A - 1)(2cos2A + 1)(2cos4A - 1)(2cos8A - 1) = (2cos2A - 1)(2cos2A + 1)(2cos4A - 1)(2cos8A - 1)
`\checkmark`