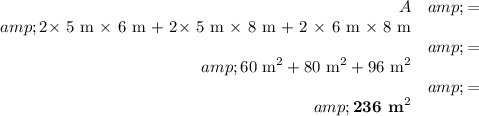Question

All the edges of a cube have the same length. Tony claims that the formula SA = 6s, where s is the length of

each side of the cube, can be used to calculate the surface area of a cube.
a. Draw the net of a cube to determine if Tony's formula is correct.
b. Why does this formula work for cubes?
Frances believes this formula can be applied to calculate the surface area of any rectangular prism. Is
she correct? Why or why not?
d. Using the dimensions of Length, Width and Height, create a formula that could be used to calculate the
surface area of any rectangular prism, and prove your formula by calculating the surface area of a
rectangular prism with dimensions L = 5m, W = 6m and H=8m.

Answer 1

Here's what I get

Explanation:

a. Net of a cube

Fig. 1 is the net of a cube

b. Does the formula work?

Tony's formula works if you ignore dimensions.

There are six squares in the net of a cube.

If each side has a unit length s, the total area of the cube is 6s.

c. Will the formula work for any rectangular prism?

No, because a rectangular prism has sides of three different lengths — l, w, and h — as in Fig. 2.

d. Area of a rectangular prism

A rectangular prism has six faces.

A top (T) and a bottom (b) — A = 2×l×w

A left (L) and a right (R) — A = 2×l×h

A front (F) and a back (B) — A = 2×w×h

Total area = 2lw + 2lh + 2wh

If l = 5 m, w = 6 m and h = 8 m,

`\begin{array}{rl}A &=& \text{2$*$ 5 m $*$ 6 m + 2$*$ 5 m $*$ 8 m + 2 $*$ 6 m $*$ 8 m}\\&=& \text{60 m}^(2) + \text{80 m}^(2) + \text{96 m}^(2)\\&=& \textbf{236 m}^(2)\\\end{array}`