Answer:
Option (3)
Explanation:
This question is not complete; here is the complete question.
Triangle A″B″C″ is formed by a reflection over y = −3 and dilation by a scale factor of 2 from the origin. Which equation shows the correct relationship between ΔABC and ΔA″B″C″?
Coordinates of the vertices of the triangle ABC are,
A(-3, 3), B(1, -3) and C(-3, -3)
When triangle ABC is reflected over y = -3
Coordinates of the image triangle A'B'C' will be.
A(-3, 3) → A'(-3, -9)
B(1, -3) → B'(1, -3)
C(-3, -3) → C'(-3, -3)
Further ΔA'B'C' is dilated by a scale factor of 2 about the origin then the new vertices of image triangle A"B"C" will be,
Rule for the dilation will be,
(x, y) → (kx, ky) [where 'k' is the scale factor]
A'(-3, -9) → A"(-6, -18)
B'(1, -3) → B"(2, -6)
C'(-3, -3) → C"(-6, -6)
Length of AB =
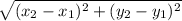
=

=

=
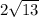
Length of A"B" =
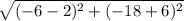
=

=
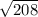
=

Therefore,
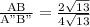

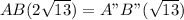
Option (3) is the answer.