Question

Triangle A″B″C″ is formed by a reflection over y = −3 and dilation by a scale factor of 2 from the origin. Which equation shows the correct relationship between ΔABC and ΔA″B″C″? coordinate plane with triangle ABC at A negative 3 comma 3, B 1 comma negative 3, and C negative 3 comma negative 3

Answer 1

Option (3)

Explanation:

This question is not complete; here is the complete question.

Triangle A″B″C″ is formed by a reflection over y = −3 and dilation by a scale factor of 2 from the origin. Which equation shows the correct relationship between ΔABC and ΔA″B″C″?

Coordinates of the vertices of the triangle ABC are,

A(-3, 3), B(1, -3) and C(-3, -3)

When triangle ABC is reflected over y = -3

Coordinates of the image triangle A'B'C' will be.

A(-3, 3) → A'(-3, -9)

B(1, -3) → B'(1, -3)

C(-3, -3) → C'(-3, -3)

Further ΔA'B'C' is dilated by a scale factor of 2 about the origin then the new vertices of image triangle A"B"C" will be,

Rule for the dilation will be,

(x, y) → (kx, ky) [where 'k' is the scale factor]

A'(-3, -9) → A"(-6, -18)

B'(1, -3) → B"(2, -6)

C'(-3, -3) → C"(-6, -6)

Length of AB =
`√((x_2-x_1)^2+(y_2-y_1)^2)`

=
`√((-3-1)^2+(3+3)^2)`

=
`√(52)`

=
`2√(13)`

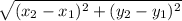
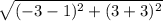
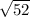
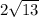
Length of A"B" =
`√((-6-2)^2+(-18+6)^2)`

=
`√(64+144)`

=
`√(208)`

=
`4√(13)`

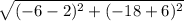
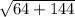
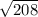
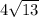
Therefore,
`\frac{\text{AB}}{\text{A`

`\frac{\text{AB}}{\text{A`

`AB(2√(13))=A`

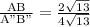
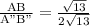
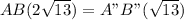
Option (3) is the answer.