Question

Express the product of z1 and z2 in standard form given that
`z_(1) = 6[cos((2\pi )/(5)) + isin((2\pi )/(5))]` and
`z_(2) = 2√(2) [cos((-\pi )/(2)) + isin((-\pi )/(2))]`

Answer 1

Solution : 5.244 - 16.140i

Explanation:

If we want to express the two as a product, we would have the following expression.

`-6\left[\cos \left((2\pi )/(5)\right)+i\sin \left((2\pi )/(5)\right)\right]\cdot 2√(2)\left[\cos \left((-\pi )/(2)\right)+i\sin \left((-\pi \:)/(2)\right)\right]`

Now we have two trivial identities that we can apply here,

( 1 ) cos(- π / 2) = 0,

( 2 ) sin(- π / 2) = - 1

Substituting them,

=
`-6\cdot \:2√(2)\left(0-i\right)\left(\cos \left((2\pi )/(5)\right)+i\sin \left((2\pi )/(5)\right)\right)`

=
`-12√(2)\sin \left((2\pi )/(5)\right)+12√(2)\cos \left((2\pi )/(5)\right)i`

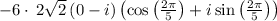
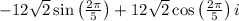
Again we have another two identities we can apply,

( 1 ) sin(x) = cos(π / 2 - x )

( 2 ) cos(x) = sin(π / 2 - x )

`\sin \left((2\pi )/(5)\right)=\cos \left((\pi )/(2)-(2\pi )/(5)\right) = \frac{√(2)\sqrt{5+√(5)}}{4}`

`\cos \left((2\pi )/(5)\right)=\sin \left((\pi )/(2)-(2\pi )/(5)\right) = \frac{√(2)\sqrt{3-√(5)}}{4}`

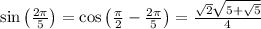
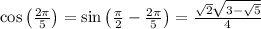
Substitute,

`-12√(2)(\frac{√(2)\sqrt{5+√(5)}}{4}) + 12√(2)(\frac{√(2)\sqrt{3-√(5)}}{4})`

=
`-6\sqrt{5+√(5)}+6\sqrt{3-√(5)} i`

=
`-16.13996 + 5.24419i`

=
`5.24419i - 16.13996`

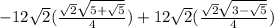
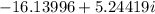
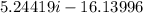
As you can see option d is the correct answer. 5.24419 is rounded to 5.244, and 16.13996 is rounded to 16.14.