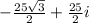Question

Write the polar form of a complex number in standard form for
`25[cos((5\pi )/(6)) + isin((5\pi )/(6))]`

Answer 1

Standard Complex Form :
`-(25√(3))/(2)+(25)/(2)i`

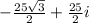
Explanation:

We want to rewrite this expression in standard complex form. Let's first evaluate cos(5π / 6). Remember that cos(x) = sin(π / 2 - x). Therefore,

cos(5π / 6) = sin(π / 2 - 5π / 6),

π / 2 - 5π / 6 = - π / 3,

sin(- π / 3) = - sin(π / 3)

And we also know that sin(π / 3) = √3 / 2. So - sin(π / 3) = - √3 / 2 = cos(5π / 6).

Now let's evaluate the sin(5π / 6). Similar to cos(x) = sin(π / 2 - x), sin(x) = cos(π / 2 - x). So, sin(5π / 6) = cos(- π / 3). Now let's further simplify from here,

cos(- π / 3) = cos(π / 3)

We know that cos(π / 3) = 1 / 2. So, sin(5π / 6) = 1 / 2

Through substitution we receive the expression 25( - √3 / 2 + i(1 / 2) ). Further simplification results in the following expression. As you can see your solution is option a.

`-(25√(3))/(2)+(25)/(2)i`