Answer:
a) The magnitude of the friction force is 55.851 newtons, b) The speed of the crate when it reaches the bottom of the ramp is 2.526 meters per second.
Step-by-step explanation:
a) This situation can be modelled by the Principle of Energy Conservation and the Work-Energy Theorem, where friction represents the only non-conservative force exerting on the crate in motion. Let consider the bottom of the straight ramp as the zero point. The energy equation for the crate is:
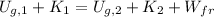
Where:
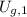 ,
,
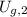 - Initial and final gravitational potential energy, measured in joules.
- Initial and final gravitational potential energy, measured in joules.
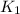 ,
,
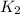 - Initial and final translational kinetic energy, measured in joules.
- Initial and final translational kinetic energy, measured in joules.
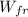 - Work losses due to friction, measured in joules.
- Work losses due to friction, measured in joules.
By applying the defintions of translational kinetic and gravitational potential energies and work, this expression is now expanded:
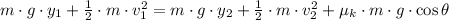
Where:
 - Mass of the crate, measured in kilograms.
- Mass of the crate, measured in kilograms.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 ,
,
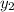 - Initial and final height of the crate, measured in meters.
- Initial and final height of the crate, measured in meters.
 ,
,
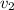 - Initial and final speeds of the crate, measured in meters per second.
- Initial and final speeds of the crate, measured in meters per second.
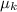 - Kinetic coefficient of friction, dimensionless.
- Kinetic coefficient of friction, dimensionless.
 - Ramp inclination, measured in sexagesimal degrees.
- Ramp inclination, measured in sexagesimal degrees.
The equation is now simplified and the coefficient of friction is consequently cleared:
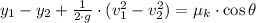
![\mu_(k) = (1)/(\cos \theta) \cdot \left[y_(1)-y_(2)+(1)/(2\cdot g)\cdot (v_(1)^(2)-v_(2)^(2)) \right]](https://img.qammunity.org/2021/formulas/physics/college/qkiw834be3pta0bjw94n8latxpqcyiwij4.png)
The final height of the crate is:

If
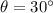 ,
,
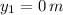 ,
,
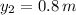 ,
,
 ,
,
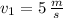 and
and
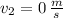 , the coefficient of friction is:
, the coefficient of friction is:
![\mu_(k) = (1)/(\cos 30^(\circ))\cdot \left\{0\,m-0.8\,m+(1)/(2\cdot \left(9.807\,(m)/(s^(2)) \right))\cdot \left[\left(5\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right] \right\}](https://img.qammunity.org/2021/formulas/physics/college/a64ronym20cvnoi9cguxqtamvsqus609ec.png)
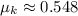
Then, the magnitude of the friction force is:

If
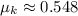 ,
,
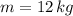 ,
,
 and
and
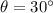 , the magnitude of the force of friction is:
, the magnitude of the force of friction is:
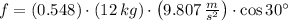
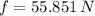
The magnitude of the force of friction is 55.851 newtons.
b) The energy equation of the situation is:
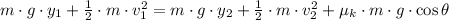
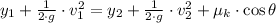
Now, the final speed is cleared:
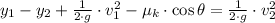
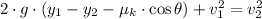

Given that
 ,
,
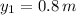 ,
,
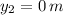 ,
,
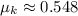 ,
,
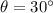 and
and
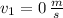 , the speed of the crate at the bottom of the ramp is:
, the speed of the crate at the bottom of the ramp is:
![v_(2)=\sqrt{2\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot [0.8\,m-0\,m-(0.548)\cdot \cos 30^(\circ)]+\left(0\,(m)/(s) \right)^(2)}](https://img.qammunity.org/2021/formulas/physics/college/2f45qgx999tufwidm1q3zpclqn6hmvhzln.png)
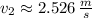
The speed of the crate when it reaches the bottom of the ramp is 2.526 meters per second.