Question

Following is a portion of the regression output for an application relating maintenance expense (dollars per month) to usage (hours per week) for a particular brand of computer terminal.

ANOVA
df SS MS F Significance F
Regression 1 1575.76
Residual 8 349.14
Total 9 1924.90
Coefficient Standard Error t Stat P-value
Intercept 6.1092 0.9361
Usage 0.8931 0.149
A) Write the estimated regression equation (to 4 decimals).
B) Use a t test to determine whether monthly maintenance expense is related to usage at the .05 level of significance (to 2 decimals, if necessary).
1. Reject the null hypothesis
2. Do not reject the null hypothesis
C) Monthly maintenance expense​______to usage.
1. Is related
2. Is not related
D) Did the estimated regression equation provide a good fit?
1. yes
2. no
E) Explain.

Answer 1

Explained below.

Explanation:

The ANOVA and Regression output for an application relating maintenance expense (dollars per month) to usage (hours per week) for a particular brand of computer terminal is provided.

(A)

The estimated regression equation equation is:

`y=6.1092+0.8931x`

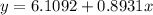
Here,

y = maintenance expense (dollars per month)

x = usage (hours per week) for a particular brand of computer terminal

(B)

Consider the Regression output.

The hypothesis to test whether monthly maintenance expense is related to usage is:

H₀: The monthly maintenance expense is not related to usage, i.e. β = 0.

Hₐ: The monthly maintenance expense is related to usage, i.e. β ≠ 0.

Compute the test statistic as follows:

`t=(b)/(S.E._(b))=(0.8931)/(0.149)=5.99`

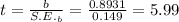
Compute the p-value as follows:

`p-value=2* P (t_(8)<5.99}=0.00033`

The null hypothesis will be rejected if the p-value is less than the significance level.

p-value = 0.00033 < α = 0.05

Reject the null hypothesis.

(C)

Monthly maintenance expense​ is related to usage.

(D)

Yes, the estimated regression equation provide a good fit.

Since the regression coefficient is significant it can be concluded that the regression equation estimated is a good fit.