Question

A Van de Graaff generator produces a beam of 2.02-MeV deuterons, which are heavy hydrogen nuclei containing a proton and a neutron.

A) If the beam current is 10.0 μA, how far apart are the deuterons?
B) Is the electrical force of repulsion among them a significant factor in beam stability? Explain.

Answer 1

A) The distance of the deuterons from one another = 2.224× 10⁻⁷ m

B) The electrical force of repulsion among them shows a small effect in beam stability.

Step-by-step explanation:

Given that:

A Van de Graaff generator produces a beam of 2.02-MeV deuterons

If the beam current is 10.0 μA, the distance of the deuterons from one another can be determined by using the concept of kinetic energy of the generator.

`\mathtt{K.E = (1)/(2)mv^2}`

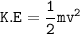
2 K.E = mv²

`\mathtt{v^2 = (2 K.E )/(m)}`

`\mathtt{v =\sqrt{ (2 K.E )/(m)}}`

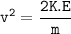
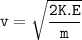
so, v is the velocity of the deuterons showing the distance of the deuterons apart from one another.

`\mathtt{v =\sqrt{ \frac{2 (2.02 \ MeV) * (10^6 \ eV)/( 1 \ MeV) * (1.60 * 10^(-19) \ J )/(1 \ eV) }{ 3.34 * 10^ {-27} \ kg}}}`

`\mathtt{v =\sqrt{ \frac{6.464 * 10^(-13) \ J }{ 3.34 * 10^ {-27} \ kg}}}`

v = 13911611.49 m/s

v = 1.39 × 10⁷ m/s

So, If the beam current is 10.0 μA.

We all know that:

`I = (q)/(t)`

`t = (q)/(I)`

`\mathtt{ t = (1.6 * 10 ^(-19) \ C)/(10.0 * 10^(-6) \ A)}`

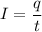
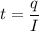
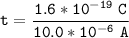
t = 1.6 × 10⁻¹⁴ s

Finally, the distance of the deuterons from one another = v × t

the distance of the deuterons from one another = (1.39 × 10⁷ m/s × 1.6 × 10⁻¹⁴ s)

the distance of the deuterons from one another = 2.224× 10⁻⁷ m

B) Is the electrical force of repulsion among them a significant factor in beam stability? Explain.

The electrical force of repulsion among them shows a small effect in beam stability. This is because, one nucleus tends to put its nearest neighbor at potential V = (k.E × q) / r = 7.3e⁻⁰³ V. This is very small compared to the 2.02-MeV accelerating potential, Thus, repulsion within the beam is a small effect.