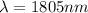Answer:
The wavelength is
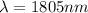
Step-by-step explanation:
From the question we are told that
The wavelength of the light is
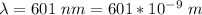
The distance of the screen is D = 3.0 m
The fringe width is
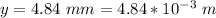
Generally the fringe width for a bright fringe is mathematically represented as
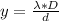
=>
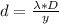
=>
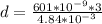
=>
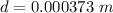
Generally the fringe width for a dark fringe is mathematically represented as
![y_d = [m + (1)/(2) ] * (\lambda D )/(d )](https://img.qammunity.org/2021/formulas/physics/college/p0sh6bci3rfie9sc7gxhix6n4upvwpiztf.png)
Here m = 0 for first order dark fringe
So
![y_d = [0 + (1)/(2) ] * (\lambda D )/(d )](https://img.qammunity.org/2021/formulas/physics/college/iw6rpgora49rqn69it07tcvblsbyhfwbys.png)
looking at which we see that
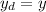
![4.84 *10^(-3) = [0 + (1)/(2) ] * (\lambda * 3 )/( 0.000373 )](https://img.qammunity.org/2021/formulas/physics/college/cm9ussn8w7kyhg7l90w5l6mgfe3485890u.png)
=>
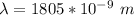
=>