Question

You check 20 batteries.Fourteen of the batteries do not have a charge. What is the experimental probability that the next battery you check does not have a charge?

Answer 1

`(7)/(10)`

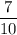
Explanation:

Given that

Number of batteries that do not have a charge = 14

Total number of batteries = 20

To find:

Experimental probability that the next battery checked does not have a charge = ?

Solution:

First of all, let us learn about the definition of experimental probability.

Probability is the chances of happening of an event.

Formula for probability of happening of an event E is given as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

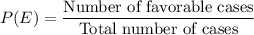
Here we have to find the probability of checking a battery that has no charge.

So, number of favorable cases = Number of batteries that do not have a charge = 14

AND

Total Number of cases = Total number of batteries to be checked = 20

So, the required probability is:

`(14)/(20) = \bold{(7)/(10)}`