Answer:
The options are not visible enough (See Explanation)
Explanation:
Given
x:- 1 || 2 || 3 || 4 || 5
y:- 13 || 22 || 37 || 58 || 85
Required
Determine if the function is quadratic
Calculate the difference between the values of y
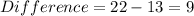
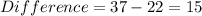
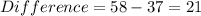

The resulting difference are: 9 || 15 || 21 || 27
Next; Calculate the difference between the difference of values of y
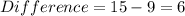
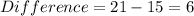
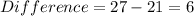
The resulting difference are: 6 || 6 || 6
For the function to be quadratic, the above difference must be the same and since they are the same (6), then the function represents a quadratic function.