Answer:
- The wavelength of this light is approximately
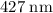 (
(
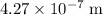 .)
.) - The distance between the first and central maxima is approximately
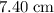 (about twice the distance between the first dark fringe and the central maximum.)
(about twice the distance between the first dark fringe and the central maximum.)
Step-by-step explanation:
Wavelength
Convert all lengths to meters:
- Separation of the two slits:
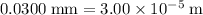 .
. - Distance between the first dark fringe and the center of the screen:
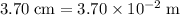 .
.
Refer to the diagram attached (not to scale.) Assuming that the screen is parallel to the line joining the two slits. The following two angles are alternate interior angles and should be equal to each other:
- The angle between the filter and the beam of light from the lower slit, and
- The angle between the screen and that same beam of light.
These two angles are marked with two grey sectors on the attached diagram. Let the value of these two angles be
 .
.
The path difference between the two beams is approximately equal to the length of the segment highlighted in green. In order to produce the first dark fringe from the center of the screen (the first minimum,) the length of that segment should be
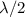 (one-half the wavelength of the light.)
(one-half the wavelength of the light.)
Therefore:
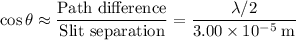 .
.
On the other hand:
 .
.
Because the cotangent of
 is very close to zero,
is very close to zero,
 .
.
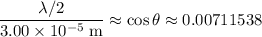 .
.
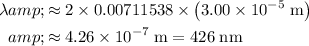 .
.
Distance between two adjacent maxima
If the path difference is increased by one wavelength, then the intersection of the two beams would move from one bright fringe to the next one.
- The path difference required for the central maximum is
 .
. - The path difference required for the first maximum is
 .
. - The path difference required for the second maximum is
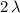 .
.
On the other hand, if the distance between the maximum and the center of the screen is much smaller than the distance between the screen and the filter, then:
 .
.
Under that assumption, the distance between the maximum and the center of the screen is approximately proportional to the path difference. The distance between the image (the first minimum) and the center of the screen is
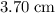 when the path difference is
when the path difference is
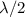 . The path difference required for the first maximum is twice as much as that. Therefore, the distance between the first maximum and the center of the screen would be twice the difference between the first minimum and the center of the screen:
. The path difference required for the first maximum is twice as much as that. Therefore, the distance between the first maximum and the center of the screen would be twice the difference between the first minimum and the center of the screen:
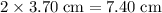 .
.