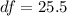Answer:
a

b
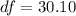
c
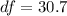
d
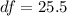
Explanation:
Generally degree of freedom is mathematically represented as
![df = ( [( s^2_i )/(m) + ( s^2_j )/(n) ]^2 )/( ( [ (s^2_i)/(m) ]^2 )/(m-1 ) +( [ (s^2_j)/(n) ]^2 )/(n-1 ) )](https://img.qammunity.org/2021/formulas/mathematics/college/fprswc09l5tvkvs607iyjbttfw7rfrt6q7.png)
Considering a
a) m = 12, n = 15, s1 = 4.0, s2 = 6.0
![df = ( [( 4^2 )/(12) + ( 6^2 )/(15) ]^2 )/( ( [ (4^2)/(12) ]^2 )/(12-1 ) +( [ (6^2)/(15) ]^2 )/(15-1 ) )](https://img.qammunity.org/2021/formulas/mathematics/college/19zih838gsjzsvaiyqoaihdk0ja91fvuqh.png)

Considering b
(b) m = 12, n = 21, s1 = 4.0, s2 = 6.0
![df = ( [( 4^2 )/(12) + ( 6^2 )/(21) ]^2 )/( ( [ (4^4)/(12) ]^2 )/(12-1 ) +( [ (6^2)/(21) ]^2 )/(21-1 ) )](https://img.qammunity.org/2021/formulas/mathematics/college/8x23196celihmeqzxszh7m8qmtaft7o636.png)
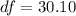
Considering c
(c) m = 12, n = 21, s1 = 3.0, s2 = 6.0
![df = ( [( 3^2 )/(12) + ( 6^2 )/(21) ]^2 )/( ( [ (3^4)/(12) ]^2 )/(12-1 ) +( [ (6^2)/(21) ]^2 )/(21-1 ) )](https://img.qammunity.org/2021/formulas/mathematics/college/d2lmwuw5r0o840yf8d94f6k1wh7whzuezy.png)
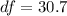
Considering c
(d) m = 10, n = 24, s1 = 4.0, s2 = 6.0
![df = ( [( 4^2 )/(10) + ( 6^2 )/(24) ]^2 )/( ( [ (4^2)/(10) ]^2 )/(10-1 ) +( [ (6^2)/(24) ]^2 )/(24-1 ) )](https://img.qammunity.org/2021/formulas/mathematics/college/bsbpq4m0f6bfl32vbmxh70v0tngsd0y1dj.png)