Answer:
x = 2√41 m
Explanation:
Since the triangle is a right angled triangle we can use Pythagoras theorem to find the missing side x
Using Pythagoras theorem we have
a² = b² + c²
where a is the hypotenuse
From the question x is the hypotenuse
So we have
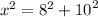

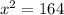
Find the square root of both sides
We have the final answer as
x = 2√41 m
Hope this helps you