Question

Y = 0.2(0.35)^t decay rate

Answer 1

The given expression
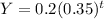`\(Y = 0.2(0.35)^t\)` represents an exponential decay model, where
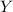`\(Y\)` is the quantity at time \(t\), the initial quantity
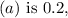`(\(a\)) is \(0.2\),` and the decay rate
`(\(r\)) is \(0.35\).`

Step-by-step explanation:

The provided expression follows the general form of an exponential decay model:
`\(Y = a(1 - r)^t\)`. Let's break down the components of this model with the given values:

1. Initial Quantity
`(\(a\))`:

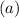• In the expression
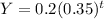  `\(Y = 0.2(0.35)^t\)`, the initial quantity
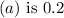  `(\(a\)) is \(0.2\)`. This represents the quantity at the beginning of the decay process.

2. Decay Rate
`(\(r\))`:

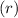• The decay rate
  `(\(r\)) is \(0.35\)`. This indicates that with each unit of time, the quantity decreases by
  `\(35\%\)`. The term
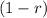  `\((1 - r)\)` is the decay factor.

3. Time
`(\(t\))`:

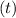The variable
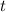`\(t\)` represents time, determining how many units of time have passed since the start of the decay process.

4. Calculation:

• If we want to find the quantity
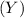  `(\(Y\))` at a specific time
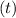  `(\(t\))`, we substitute the values into the expression. For example, if
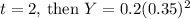  `\(t = 2\), then \(Y = 0.2(0.35)^2\)`would give the quantity at time 2.

Detailed calculation:
`\(Y = 0.2(0.35)^t\)`

• For
  `\(t = 1\): \(Y = 0.2(0.35)^1 = 0.07\)`
• For
  `\(t = 2\): \(Y = 0.2(0.35)^2 = 0.0245\)`
• For
  `\(t = 3\): \(Y = 0.2(0.35)^3 = 0.00857\)`

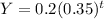
In summary, the expression
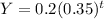`\(Y = 0.2(0.35)^t\)` provides a way to calculate the quantity at different points in time in an exponential decay process. The decay rate of
`\(35\%\)` ensures a gradual reduction in the quantity over time, and the initial quantity of
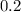`\(0.2\)` determines the starting point of the decay.

Complete the question:

What does the expression
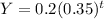`\(Y = 0.2(0.35)^t\)` represent in terms of exponential decay, and how can it be used to calculate the quantity at different points in time?

Answer 2

Step-by-step explanation:

At 1 year old it is: e1 = 2.7 mm high ... really tiny!

At 5 years it is: e5 = 148 mm high ... as high as a cup

At 10 years: e10 = 22 m high ... as tall as a building

At 15 years: e15 = 3.3 km high ... 10 times the height of the Eiffel Tower

At 20 years: e20 = 485 km high ... up into space!