Question

Given the equations, which of the following represents z1 * z2? Using the same values in #6, which of the following represents z1/z2 in standard form?

The selected answers are incorrect.

Answer 1

First Attachment : Option A,

Second Attachment : Option C

Explanation:

We are given that,

z₁ =
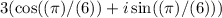`3(\cos ((\pi )/(6))+i\sin ((\pi )/(6)))` and z₂ =
`4(\cos ((\pi )/(3))+i\sin ((\pi )/(3)))`

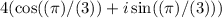
Therefore if we want to determine z₁( z₂ ), we would have to find the trigonometric form of the following expression,

`3(\cos ((\pi )/(6))+i\sin ((\pi )/(6)))*4(\cos ((\pi )/(3))+i\sin ((\pi )/(3)))`

( Combine expressions )

=
`12(\cos ( \pi /6+\pi / 3 ) + i\sin (\pi /6 +\pi / 3 )`

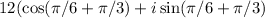
( Let's now add
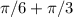`\pi / 6 + \pi / 3`, further simplifying this expression )

`(\pi )/(6)+(\pi )/(3) = (\pi )/(6)+(\pi 2)/(6) = (\pi +\pi 2)/(6) = (3\pi )/(6) = \pi / 2`

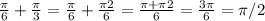
( Substitute )

`12(\cos ( \pi /2 ) + i\sin ( \pi /2 ) )`

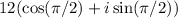
And therefore the correct solution would be option a, for the first attachment.

______________________________________________

For this second attachment, we would have to solve for the following expression,

`(3\left(\cos \left((\pi \:)/(6)\right)+i\sin \left((\pi \:)/(6)\right)\right))/(4\left(\cos \left((\pi \:)/(3)\right)+i\sin \left((\pi \:)/(3)\right)\right))`

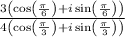
From which we know that cos(π/6) = √3 / 2, sin(π/6) = 1 / 2, cos(π/3) = 1 / 2, and sin(π/3) = √3 / 2. Therefore,

`\:(3\left(\cos \left((\pi )/(6)\right)+i\sin \left((\pi )/(6)\right)\right))/(4\left(\cos \left((\pi )/(3)\right)+i\sin \left((\pi )/(3)\right)\right)):\quad (3√(3))/(8)-i(3)/(8)`

`(3√(3))/(8)-i(3)/(8) = (3√(3))/(8)-(3)/(8)i`

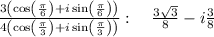
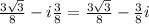
Our solution for the second attachment will be option c.