Question

You sell tickets at school for fundraisers. You sold car wash tickets, silly string fight tickets and dance tickets – for a total of 380 tickets sold. The car wash tickets were $5 each, the silly sting fight tickets were $3 each and the dance tickets were $10 each. If you sold twice as many silly string tickets as car wash tickets, and you have $1460 total. Write the matrix in the box below. Write the solution set for this system and include any necessary work.

Answer 1

Matrix :

`\begin{bmatrix}1&1&1&|&380\\ 5&3&10&|&1460\\ -2&1&0&|&0\end{bmatrix}`

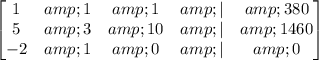
Solution Set : { x = 123, y = 246, z = 11 }

Explanation:

Let's say that x represents the number of car wash tickets, y represents the number of silly sting fight tickets, and z represents the number of dance tickets. We know that the total tickets = 380, so therefore,

x + y + z = 380,

And the car wash tickets were $5 each, the silly sting fight tickets were $3 each and the dance tickets were $10 each, the total cost being $1460.

5x + 3y + 10z = 1460

The silly string tickets were sold for twice as much as the car wash tickets.

y = 2x

Therefore, if we allign the co - efficients of the following system of equations, we get it's respective matrix.

System of Equations :

`\begin{bmatrix}x+y+z=380\\ 5x+3y+10z=1460\\ y=2x\end{bmatrix}`

Matrix :

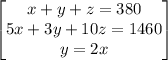
`\begin{bmatrix}1&1&1&|&380\\ 5&3&10&|&1460\\ -2&1&0&|&0\end{bmatrix}`

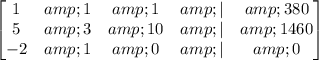
Let's reduce this matrix to row - echelon form, receiving the number of car wash tickets, silly sting fight tickets, and dance tickets,

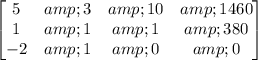`\begin{bmatrix}5&3&10&1460\\ 1&1&1&380\\ -2&1&0&0\end{bmatrix}` - Swap Matrix Rows

`\begin{bmatrix}5&3&10&1460\\ 0&(2)/(5)&-1&88\\ -2&1&0&0\end{bmatrix}` - Cancel leading Co - efficient in second row

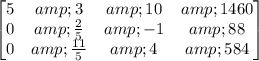`\begin{bmatrix}5&3&10&1460\\ 0&(2)/(5)&-1&88\\ 0&(11)/(5)&4&584\end{bmatrix}` - Cancel leading Co - efficient in third row

`\begin{bmatrix}5&3&10&1460\\ 0&(11)/(5)&4&584\\ 0&(2)/(5)&-1&88\end{bmatrix}` - Swap second and third rows

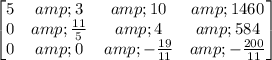`\begin{bmatrix}5&3&10&1460\\ 0&(11)/(5)&4&584\\ 0&0&-(19)/(11)&-(200)/(11)\end{bmatrix}` - Cancel leading co - efficient in row three

And we can continue, canceling the leading co - efficient in each row until this matrix remains,

`\begin{bmatrix}1&0&0&|&(2340)/(19)\\ 0&1&0&|&(4680)/(19)\\ 0&0&1&|&(200)/(19)\end{bmatrix}`

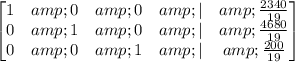
x = 2340 / 19 = ( About ) 123 car wash tickets sold, y= 4680 / 19 =( About ) 246 silly string fight tickets sold, z = 200 / 19 = ( About ) 11 tickets sold