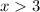Answer:
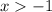 or
or
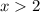 or
or
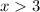
Explanation:
Given
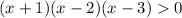
Required
Solve; with steps
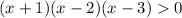
Start by splitting the inequality as follows
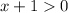 or
or
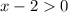 or
or
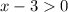
Solve the inequalities one after the other
Solving:
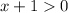
Subtract 1 from both sides
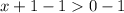
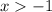
Solving:
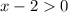
Add 2 to both sides
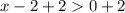
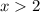
Solving:
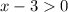
Add 3 to both sides
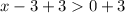
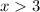
Hence, the solution to the inequality is
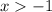 or
or
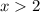 or
or