Question

Question (2)

ASAP Please help.

Construct the "Square root spiral". Take a large sheet of paper and construct the "Square root spiral" in the following fashion.

Start with a point O and draw a line segment
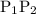
`\rm{P_(1) P_(2)}` perpendicular to
`\rm{OP_(1)}` of unit length. Now draw a line segment
`\rm{P_(2) P_(3)}` perpendicular to
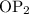
`\rm{OP_(2)}` . Then draw a line segment
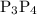
`\rm{P_(3) P_(4)}` perpendicular to
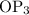
`\rm{OP_(3)}`. Continuing in this matter, you get line segment of unit length perpendicular to
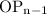
`\rm{OP_(n-1)}`. In this manner, you will have created the points
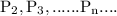
`\rm{P_(2), P_(3),...... P_(n)....}`, and joined them to create a beautiful spiral depicting
`\rm{√(2), √(3), √(4),...}`



​

Answer 1

The "square root spiral," donned the "Spiral of Theodorus" was created by Theodorus to visualize a set of 17 isosceles triangles where
`n` is equal to a value between one and seventeen.

• The central angle is attached to a central point, and the side opposite of the central angle is always equal to 1.
• The hypotenuse of the triangle is equivalent to
  `√(n+1)`. The hypotenuse becomes a leg for the next triangle.

I have attached an image of the Square Root spiral below.