The weight of a small starbucks coffee is a normally distributed random variable with a mean of 325 grams and a standard deviation of 10 grams. Find the weight that corresponds to each event (round your final answers to 2 decimal places)
a. Highest 10 percent
b. Middle 50 percent
Answer:
the weight that corresponds to Highest 10% = 337.8
the weight that corresponds to Middle 50 % lies between 318.26 and 331.74
Explanation:
From the information provided for us:
we have the mean = 325
the standard deviation = 10
The objective is to find the weight that corresponds to each event i.e for event (a) , highest 10%
So;
The probability of P (Z > z) = 10%
Same as:
0.1 = 1 - P( Z < z)
P( Z < z) = 1 - 0.1
P( Z < z) = 0.9
From the standard normal tables for z;
P( Z < 1.28) = 0.9
z = 1.28
Similarly. from the z formula; we have:
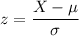
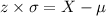
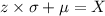
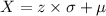
X = (1.28 × 10) + 325
X = 12.8 + 325
X = 337.8
Therefore, the weight that corresponds to Highest 10% = 337.8
b. the weight that corresponds to Middle 50 % can be computed as follows:
the region of z values at 0.50 lies between -0.674 and +0.674
from the z formula; we have:
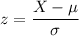
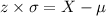
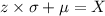
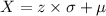
X = -0.674 × 10 + 325 and X = 0.674 × 10 + 325
X = - 6.74 + 325 and X = 6.74 + 325
X = 318.26 and X = 331.74
the weight that corresponds to Middle 50 % lies between 318.26 and 331.74