Question

Sixty-five percent of employees make judgements about their co-workers based on the cleanliness of their desk. You randomly select 8 employees and ask them if they judge co-workers based on this criterion. The random variable is the number of employees who judge their co-workers by cleanliness. Which outcomes of this binomial distribution would be considered unusual?

Answer 1

The outcomes of this binomial distribution that would be considered unusual is {0, 1, 2, 8}.

Explanation:

The outcomes provided are:

(A) 0, 1, 2, 6, 7, 8

(B) 0, 1, 2, 7, 8

(C) 0, 1, 7, 8

(D) 0, 1, 2, 8

Solution:

The random variable X can be defined as the number of employees who judge their co-workers by cleanliness.

The probability of X is:

P (X) = 0.65

The number of employees selected is:

n = 8

An unusual outcome, in probability theory, has a probability of occurrence less than or equal to 0.05.

Since outcomes 0 and 1 are contained in all the options, we will check for X = 2.

Compute the value of P (X = 2) as follows:

`P(X=2)={8\choose 2}(0.65)^(2)(0.35)^(8-2)`

`=28* 0.4225* 0.001838265625\\=0.02175\\\approx 0.022<0.05`

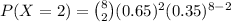
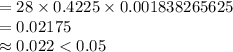
So X = 2 is unusual.

Similarly check for X = 6, 7 and 8.

P (X = 6) = 0.2587 > 0.05

X = 6 not unusual

P (X = 7) = 0.1373 > 0.05

X = 7 not unusual

P (X = 8) = 0.0319

X = 8 is unusual.

Thus, the outcomes of this binomial distribution that would be considered unusual is {0, 1, 2, 8}.