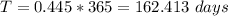Answer:
a
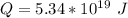
b
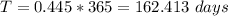
Step-by-step explanation:
From the question we are told that
The area of Manhattan is

The area of the ice is
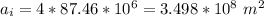
The thickness is

Generally the volume of the ice is mathematically represented is
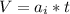
substituting value
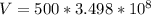
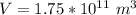
Generally the mass of the ice is
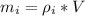
Here
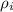 is the density of ice the value is
is the density of ice the value is
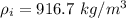
=>
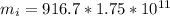
=>

Generally the energy needed for the ice to melt is mathematically represented as
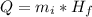
Where
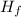 is the latent heat of fusion of ice and the value is
is the latent heat of fusion of ice and the value is
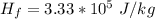
=>
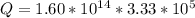
=>
Considering part b
We are told that the annual energy consumption is
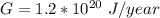
So the time taken to melt the ice is
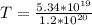
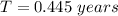
converting to days