Answer and Step-by-step explanation:
A) Probability of taken two odd numbered token without replacement:
P(3) = 2/5 = 0.4
P(7) = 1/4 = 0.25
Construct a probability distribution:
X 3 7
p(X) 0.4 0.25
B) Mean of the probability distribution:
E(X) = ∑xp
E(X) = 3*0.4 + 7*0.25
E(X) = 2.95
Variance of the probability distribution:
V(X) =
![\Sigma X^(2)p - [E(X)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/y9vphk06al501mpwogsb98gl8f285dpmju.png)
V(X) =
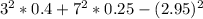
V(X) = 7.1475
Mean and variance of the probability distribution are 2.95 and 7.145, respectively.