Answer:
(i) 0.32 (ii) 0.85
(iii) 0.3412 (iv) 0.20
(v) 0.29 (vi) 0.12
Explanation:
The data provided is as follows:
Race Smoker (S) Nonsmoker (N) Row Total
White(W) 290 560 850
Black(B) 30 120 150
Column Total 320 680 1,000
(i)
Compute the value of P (S) as follows:
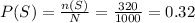
P (S) = 0.32.
(ii)
Compute the value of P (W) as follows:
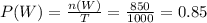
P (W) = 0.85.
(iii)
Compute the value of P (S|W) as follows:
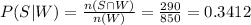
P (S|W) = 0.3412.
(iv)
Compute the value of P (S|B) as follows:
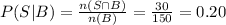
P (S|W) = 0.20.
(v)
Compute the value of P (S∩W) as follows:
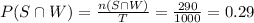
P (S∩W) = 0.29.
(vi)
Compute the value of P (N∩B) as follows:
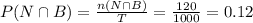
P (S∩W) = 0.12.